Реших да разкажа, за моята имплементация, на една от задачите от втората част от курса по C# в Telerik Academy, а именно примерна имплементация на алгоритъма Shunting yard, за пресмятане на аритметичен израз.
В случая като въведение в проблема, ще дам един пример, за такъв аритметичен израз и неговото пресмятане със съответните приоритети на операторите:
Важно е тук да се спомене, че най-висок приоритет имат скобите, след тях е операцията повдигане на степен (която е дясно-асоциативна за разлика от другите ляво-асоциативни операции), след това са операциите умножение и деление и накрая с най-нисък приоритет са операциите събиране и изваждане. В израза също така участва и едно-аргументната функция корен квадратен (sqrt), чийто приоритет в случая е излишно да бъде търсен, тъй като за нейния запис използваме скоби, ограждащи аргумента й.
За построяването на дървото на операциите, необходимо ни, за да знаем, коя операция да извършим първа, коя втора и така нататък, докато пресметнем целия израз, съм използвал така наречения Shunting Yard Algorithm. Цъкайки на дадения линк към wikipedia, по надолу в статията ще достигнете и до описанието на последователността на действията в самия алгоритъм, които са:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | -While there are tokens to be read: --Read a token. --If the token is a number, then add it to the output queue. --If the token is a function token, then push it onto the stack. --If the token is a function argument separator (e.g., a comma): ----Until the token at the top of the stack is a left parenthesis, pop operators off the stack onto the output queue. If no left parentheses are encountered, either the separator was misplaced or parentheses were mismatched. --If the token is an operator, o1, then: ----while there is an operator token, o2, at the top of the stack, and either o1 is left-associative and its precedence is less than or equal to that of o2, or o1 has precedence less than that of o2, pop o2 off the stack, onto the output queue; ----push o1 onto the stack. --If the token is a left parenthesis, then push it onto the stack. --If the token is a right parenthesis: ----Until the token at the top of the stack is a left parenthesis, pop operators off the stack onto the output queue. ----Pop the left parenthesis from the stack, but not onto the output queue. ----If the token at the top of the stack is a function token, pop it onto the output queue. ----If the stack runs out without finding a left parenthesis, then there are mismatched parentheses. -When there are no more tokens to read: --While there are still operator tokens in the stack: ----If the operator token on the top of the stack is a parenthesis, then there are mismatched parentheses. ----Pop the operator onto the output queue. -Exit. |
Преди да започна с имплементацията на алгоритъма, аз си създавам една структура PredefinedFunction, която ще ми описва основните параметри на всяка една предефинирана в програмата функция – брой параметри, приемаща функцията; дали е ляво или дясно асоциативна; самите действия, които ще прави функцията върху параметрите си, записани като поле от тип делегат; приоритета на конкретната функция. Ето и имплементацията на тази структура:
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | public struct PredefinedFunction { public int parametersCount; public bool isLeftAssociated; public Function.Calculate calculateFunction; public int priority; public PredefinedFunction(int parametersCount, bool isLeftAssociated, Function.Calculate calculateFunction, int priority) : this() { this.parametersCount = parametersCount; this.isLeftAssociated = isLeftAssociated; this.calculateFunction = calculateFunction; this.priority = priority; } } |
След това дефинирам класа Function, който ще съдържа речник от предефинирани функции, като всяка ще знае как да работи, благодарение на свойството Result ползващо полето делегат calculateFunction, на съответната предефинирана функция. Ето и имплементацията на този клас.
24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 | public class Function { public delegate double Calculate(double[] parameters); private double[] parameters; private string functionName; private static Dictionary<string, PredefinedFunction> functionsLibrary; static Function() { functionsLibrary = new Dictionary<string, PredefinedFunction>(); functionsLibrary.Add("+", new PredefinedFunction(2, true, new Calculate(x => x[0] + x[1]), 1)); functionsLibrary.Add("-", new PredefinedFunction(2, true, new Calculate(x => x[0] - x[1]), 1)); functionsLibrary.Add("*", new PredefinedFunction(2, true, new Calculate(x => x[0] * x[1]), 2)); functionsLibrary.Add("/", new PredefinedFunction(2, true, new Calculate(x => x[0] / x[1]), 2)); functionsLibrary.Add("^", new PredefinedFunction(2, false, new Calculate(x => Math.Pow(x[0], x[1])), 3)); functionsLibrary.Add("pow", new PredefinedFunction(2, true, new Calculate(x => Math.Pow(x[0], x[1])), 4)); functionsLibrary.Add("ln", new PredefinedFunction(1, true, new Calculate(x => Math.Log(x[0])), 4)); functionsLibrary.Add("sqrt", new PredefinedFunction(1, true, new Calculate(x => Math.Sqrt(x[0])), 4)); } public Function(string functionName) { this.functionName = functionName; this.parameters = new double[functionsLibrary[functionName].parametersCount]; } public static Dictionary<string, PredefinedFunction> Library { get { return functionsLibrary; } } public string FunctionName { get { return this.functionName; } } public double this[int index] { get { return this.parameters[index]; } set { this.parameters[index] = value; } } public int ParameterCount { get { return functionsLibrary[functionName].parametersCount; } } public int Precedence { get { return functionsLibrary[functionName].priority; } } public bool IsLeftAssociated { get { return functionsLibrary[functionName].isLeftAssociated; } } public double Result { get { return functionsLibrary[this.functionName].calculateFunction(this.parameters); } } } |
Статичния конструктор Function() има за цел да зареди речника от предефинирани функции, преди използването на класа. Тук е мястото да отбележа, че използването на този речник, свързващ символ в израза с конкретна функция, прави изключително лесно в последствие добавянето на нови и нови функции в кода. Ако искаме да добавим 1 нова функция, трябва да добавим само 1 ред към съществуващия код, описващ как е записа на тази функция в аритметичния израз и какви са нейните предефинирани характеристики (приоритет, асоциативност, конкретни пресмятания с аргументите и броя аргументи).
Тук следва да бъде спомената и имплементацията на Shunting Yard Algorithm:
166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 | public static void ShuntingYard(string token, Stack<string> output, Stack<string> operators) { #region Number double tempNumber; if (double.TryParse(token, out tempNumber)) { output.Push(token); return; } #endregion Number #region Function or Operator if (Function.Library.ContainsKey(token)) { if (Function.Library[token].priority == 4) { operators.Push(token); } else { while (IsThereHigherOperatorWaiting(token, operators)) { output.Push(operators.Pop()); } operators.Push(token); } return; } #endregion Function or Operator #region Parenthesis if (token == "(") { operators.Push(token); return; } if (token == ")") { GoToPreviousLeftParenthesisAndRemoveThem(output, operators); return; } #endregion Parenthesis #region Comma if (token == ",") { GoToPreviousLeftParenthesis(output, operators); return; } #endregion Comma } |
Имплементацията следва точно горе-описания с думи алгоритъм.
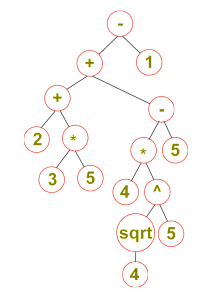
В крайна сметка тази имплементация търси последователността на сметките, които трябва да се извършат, като най-първото пресмятане, ще бъде открито последно. Поради тази причина използвам една глобална променлива от тип стек, която пълня с всеки следващ намерен от алгоритъма “ход”. Изпразвайки стека елемент по елемент в последствие аз ще получа правилната последователност на извършваните операциите, която съответства и на съответното дърво на операциите. Ето и дървото за горния пример за по-голяма яснота.
Пресмятането става посредством метода RNP (идващо от Reversed Polish Notation), който вътрешно използва метода ParseNumberOrFunction().
295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 | public static double CalculateRPN() { return ParseNumberOrFunction(); } private static double ParseNumberOrFunction() { double result = 0; if (double.TryParse(RPN.Peek(), out result)) { RPN.Pop(); return result; } Function function = new Function(RPN.Pop()); if (function.IsLeftAssociated) { for (int i = function.ParameterCount - 1; i >= 0; i--) { function[i] = ParseNumberOrFunction(); } } else { for (int i = function.ParameterCount - 1; i >= 0; i--) { function[i] = ParseNumberOrFunction(); } } result = function.Result; return result; } |
Идеята е, че се чете поредния елемент от стека RPN, който е генериран предварително от Shunting Yard алгоритъма и съхранен като глобална променлива Stack<string> RNP. Тук е редно да се спомене, че по принцип не е добре да се използва глобална променлива, което го отчитам като недостатък на кода. Това обаче може лесно да се корегира, като променливата се дефинира да речем в Main метода и после се предава като аргумент на необходимите методи. И все пак в конкретния случай съм използвал глобална променлива като едно неформално решение на проблема. При четене на съответния елемент в стека, ако той е число то то се връща като стойност на метода, а ако е функция или оператор, тогава се извиква рекурсивно същия метод за всеки от аргументите на последната извикана функция. По този начин дървото на пресмятанията се обхожда в дълбочина пресмятайки, най-накрая чрез рекурсията крайния резултат.
Ето и пълния код на моята C# имплементация:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 | using System; using System.Collections.Generic; using System.Threading; using System.Globalization; class CalculateArithmeticalExpression { public struct PredefinedFunction { public int parametersCount; public bool isLeftAssociated; public Function.Calculate calculateFunction; public int priority; public PredefinedFunction(int parametersCount, bool isLeftAssociated, Function.Calculate calculateFunction, int priority) : this() { this.parametersCount = parametersCount; this.isLeftAssociated = isLeftAssociated; this.calculateFunction = calculateFunction; this.priority = priority; } } public class Function { public delegate double Calculate(double[] parameters); private double[] parameters; private string functionName; private static Dictionary<string, PredefinedFunction> functionsLibrary; static Function() { functionsLibrary = new Dictionary<string, PredefinedFunction>(); functionsLibrary.Add("+", new PredefinedFunction(2, true, new Calculate(x => x[0] + x[1]), 1)); functionsLibrary.Add("-", new PredefinedFunction(2, true, new Calculate(x => x[0] - x[1]), 1)); functionsLibrary.Add("*", new PredefinedFunction(2, true, new Calculate(x => x[0] * x[1]), 2)); functionsLibrary.Add("/", new PredefinedFunction(2, true, new Calculate(x => x[0] / x[1]), 2)); functionsLibrary.Add("^", new PredefinedFunction(2, false, new Calculate(x => Math.Pow(x[0], x[1])), 3)); functionsLibrary.Add("pow", new PredefinedFunction(2, true, new Calculate(x => Math.Pow(x[0], x[1])), 4)); functionsLibrary.Add("ln", new PredefinedFunction(1, true, new Calculate(x => Math.Log(x[0])), 4)); functionsLibrary.Add("sqrt", new PredefinedFunction(1, true, new Calculate(x => Math.Sqrt(x[0])), 4)); } public Function(string functionName) { this.functionName = functionName; this.parameters = new double[functionsLibrary[functionName].parametersCount]; } public static Dictionary<string, PredefinedFunction> Library { get { return functionsLibrary; } } public string FunctionName { get { return this.functionName; } } public double this[int index] { get { return this.parameters[index]; } set { this.parameters[index] = value; } } public int ParameterCount { get { return functionsLibrary[functionName].parametersCount; } } public int Precedence { get { return functionsLibrary[functionName].priority; } } public bool IsLeftAssociated { get { return functionsLibrary[functionName].isLeftAssociated; } } public double Result { get { return functionsLibrary[this.functionName].calculateFunction(this.parameters); } } } public static Stack<string> RPN; static void Main() { Thread.CurrentThread.CurrentCulture = CultureInfo.InvariantCulture; PrintTestInput("2 + 3 * 5 / ( 4 - 5 ) - 1"); PrintTestInput("2 + 3 * 5 + ( 4 * pow ( ( sqrt ( 4 + ln ( 1 ) ) - 1 ) , 5 ) - 5 ) - 1"); PrintTestInput("2 + 3 * 5 + ( 4 * pow ( ( sqrt ( 4 ) ) , 5 ) - 5 ) - 1"); PrintTestInput("2 + 3 * 5 + ( 4 * ( sqrt ( 4 ) ^ 5 ) - 5 ) - 1"); PrintTestInput("2 + 3 * 5 + ( 4 * sqrt ( 4 ) ^ 5 - 5 ) - 1"); PrintTestInput("2 + 3 * 5 + ( 2 ^ 2 * sqrt ( 4 ) ^ 5 - 5 ) - 1"); PrintTestInput("2 + 3 * 5 + ( 2 ^ 2 * sqrt ( 4 ) ^ 2 ^ 2 * 2 - 5 ) - 1"); PrintTestInput("( 2 + 3 ) * 5"); } public static void PrintTestInput(string input) { Console.WriteLine("At the begining we have the input expression:\n{0}", input); RPN = GenerateRNP(input); Console.WriteLine("First we generate its Polish Notation equivalent:"); PrintRNP(); Console.WriteLine(); RPN = GenerateRNP(input); Console.WriteLine("Finally the calculated result: {0}", CalculateRPN()); Console.WriteLine(); } public static void PrintFunctionLibrary() { foreach (string name in Function.Library.Keys) { Console.WriteLine("function {0}, priority {1}", name, Function.Library[name].priority); } } public static Stack<string> GenerateRNP(string expression) { Stack<string> output = new Stack<string>(); Stack<string> operators = new Stack<string>(); string[] tokens = expression.Split(new char[] { ' ' }, StringSplitOptions.RemoveEmptyEntries); for (int i = 0; i < tokens.Length; i++) { ShuntingYard(tokens[i], output, operators); } while (operators.Count > 0) { output.Push(operators.Pop()); } return output; } public static void ShuntingYard(string token, Stack<string> output, Stack<string> operators) { #region Number double tempNumber; if (double.TryParse(token, out tempNumber)) { output.Push(token); return; } #endregion Number #region Function or Operator if (Function.Library.ContainsKey(token)) { if (Function.Library[token].priority == 4) { operators.Push(token); } else { while (IsThereHigherOperatorWaiting(token, operators)) { output.Push(operators.Pop()); } operators.Push(token); } return; } #endregion Function or Operator #region Parenthesis if (token == "(") { operators.Push(token); return; } if (token == ")") { GoToPreviousLeftParenthesisAndRemoveThem(output, operators); return; } #endregion Parenthesis #region Comma if (token == ",") { GoToPreviousLeftParenthesis(output, operators); return; } #endregion Comma } private static void GoToPreviousLeftParenthesis(Stack<string> output, Stack<string> operators) { while (operators.Count > 0) { if (operators.Peek() == "(") { return; } output.Push(operators.Pop()); } } private static void GoToPreviousLeftParenthesisAndRemoveThem(Stack<string> output, Stack<string> operators) { while (operators.Count > 0) { if (operators.Peek() == "(") { operators.Pop(); if (operators.Count > 0 && Function.Library.ContainsKey(operators.Peek())) { if (Function.Library[operators.Peek()].priority == 4) { output.Push(operators.Pop()); } } return; } output.Push(operators.Pop()); } } private static bool IsThereHigherOperatorWaiting(string token, Stack<string> operators) { if (operators.Count == 0) return false; if (Function.Library.ContainsKey(operators.Peek()) && Function.Library[operators.Peek()].priority < 4) { if (Function.Library[token].isLeftAssociated) { if (Function.Library[token].priority <= Function.Library[operators.Peek()].priority) { return true; } } else { if (Function.Library[token].priority < Function.Library[operators.Peek()].priority) { //Console.WriteLine("No left associatives in this homework!"); return true; } } } return false; } public static void PrintRNP() { while (RPN.Count > 0) { Console.Write("{0} ", RPN.Pop()); } } public static double CalculateRPN() { return ParseNumberOrFunction(); } private static double ParseNumberOrFunction() { double result = 0; if (double.TryParse(RPN.Peek(), out result)) { RPN.Pop(); return result; } Function function = new Function(RPN.Pop()); if (function.IsLeftAssociated) { for (int i = function.ParameterCount - 1; i >= 0; i--) { function[i] = ParseNumberOrFunction(); } } else { for (int i = function.ParameterCount - 1; i >= 0; i--) { function[i] = ParseNumberOrFunction(); } } result = function.Result; return result; } } |
PrintTestInput(“(2 + 3 )* 5”);
= 8
Здравей, Валентин! Благодаря за включването 🙂 Не влизам често в сайта, но ми стана любопитно като видях, че имам коментар по блог поста и реших да погледна откъде идва проблема. Самият код, който съм описал горе беше правен за едно домашно към академията на Телерик и целта беше по-скоро да се имплементира работещ алгоритъм за пресмятане на такива изрази. И реално, тествайки с “( 2 + 3 ) * 5” получавам коректен резултат 25. Когато обаче махна някой от спейсовете, както е записано горе в твоя пример “(2 + 3 )* 5”, се получава обратен полски запис “+ 3 5” тъй като тоукъните “(2” и “)*” се явяват непознати. Накратко казано – в конкретното решение нямам имплементация на tokenizer и вместо такъв изпозвам string.Split(‘ ‘) (това може да се види на ред 153 от кода). Ако вместо ред 153 се използва по-сложен tokenizer от string.Split тогава ще имам правилните token-и и съответно алгоритъма ще пресметне правилно израза :).
Между другото като се опитах да си копирам кода от сайта във Visual Studio видях известни проблеми с някои символи, както и стека по някаква причина не беше от тип generic. Фикснах тези дребни проблемчета в поста и надявам се сега кода става лесен за тестване. Добавих и твоя пример в Main функцията, където печатам на конзолата някакви тестови резултати :). Благодаря отново за коментара. Ако имаш някакви допълнителни коментари или въпроси ще се радвам да ги прочета. Държа да отбележа, че сега поглеждайки кода 1 година по-късно определено има бая неща, които бих рефакторирал (RPN стека, който не бива да е статичен и ред други глупости, които виждам, но да кажем че това са детайли :)).
Поздрави,
Деян
Здравейте,
Видях примера докато търсех нещо за “Convert string to formula” .
Трябвяше ми за форми (диалогови панели) в едно приложение.
Заказчика искаше да може да вкарва стойност или формула в
текстовото поле.
После се сетих, че може да се приложи и от командния ред на AutoCAD
при скриптове за автоматизация на конструкторския труд.
Помня, че намерих нещо подходящо и помня, че направих едно питане в
една от страниците но не си спомням вече какво избрах.
Избрах нещо и си спомням, че и аз май пипнах нещо – но общо взето
стана добре (не съм правил кой знае колко изчерпателни тестове).
Едната поръчка отпадна, а на скрипта за AutoCAD му прдстои сериозно тестване
като цяло.
Поздрави,
Лишков
Здравейте! Аз тепърва навлизам в нещата и стигнах до това решение на проблема(“( 2 + 3 ) * 5” или “(2+3)*5”):
public static Stack GenerateRNP(string expression)
{
Stack output = new Stack();
Stack operators = new Stack();
var unseparatedSymbols = new Queue();
var tokens = expression.Split().ToList();
for (int i = 0; i < tokens.Count; i++)
{
if (tokens[i].Length != 1)
{
foreach (var item in tokens[i])
{
unseparatedSymbols.Enqueue(item);
}
tokens.RemoveAt(i);
foreach (var item in unseparatedSymbols)
{
tokens.Add(item.ToString());
}
}
ShuntingYard(tokens[i].ToString(), output, operators);
}